Matematik/Matematik C/Funktioner

Funktioner

Linjära och kvadratiska funktioner

Funktionsbegreppet

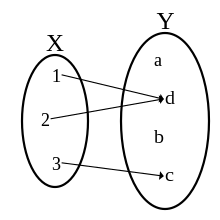
Funktioner är något vi alla stöter på överallt i vår vardag, utan att vi tänker på det. En funktion är något som för varje sak i sin in-mängd ger ett objekt i sin ut-mängd. Exempel:

Varje hus har ett antal våningar. Då är in-mängden alla möjliga hus, t ex ditt hus, eller din grannes hus. Utmängden är då ett tal. Funktionen svarar isåfall på frågan: Hur många våningar har detta hus? Oavsett vilket hus du frågar om ger funktionen ett svar.
Varje cirkel har en omkrets med en viss längd.
Varje glödlampa har en viss strömförbrukning.

För tydlighetens skull brukar man kalla varje funktion för något. Man kan kalla dem för vad som helst, men ett vanligt namn är $f$ . Indatan kallas ofta för $x$ och utdatan kallas ofta för $y$ . Man skriver detta $y=f(x)$ vilket uttalas y är en funktion f av x eller kort och gott y är f av x. Ett annat, ovanligare, sätt att skriva är $f:X\mapsto Y$ .

Linjära ekvationer

Två saker ska vara uppfyllda av en funktion, F, för att få kallas linjär.

1)

F(x+y)=F(x)+F(y)

för alla värden på x och y.

2)

F(a\cdot x)=a\cdot F(x)

för värden på konstanten a.

$y=kx+m$

Andragradsfunktioner

En andragradsfunktion är en ickelinjär funktion där y ökar/minskar exponentiellt i förhållande till x.

Ex:

F(x^2) = y

I en kurva av en andragradsfunktion kan man bestämma maximum och minimum med hjälp av derivata.

Exponential- och potensfunktioner

Potenslagarna

Logaritmer

Logaritmen för ett tal (a) är den exponent (x) som man måste upphöja ett givet tal (basen b) till för att få a
a = b^x

Vad är logaritmen bra för? Man kan förenkla multiplikationer till additioner i stället eftersom a^x $\cdot$ a^y = a^x+y. Eller som logaritmlagen säger: log a + log b = log (a $\cdot$ b)

exempel
Räkna ut 3 gånger 5 med en addition.

Addera log 3 med log 5:

0.4771212547 + 0.6989700043 = 1.176091259 vilket är värdet av log 15.

Nån gång kanske man hamnar i situationen att man vill lösa ut exponenten i ett tal. Hur gör man då?

Jo, eftersom en av logaritmlagarna säger att log aⁿ = n log a så kan log användas i ekvationen:

exempel
Bryt ut x i talet a^x = y.

Vi tar logaritmen av bägge sidor:

log a^x = log y

Skriver om det enligt logaritmlagen:

x log a = log y

och bryter ut x

x = log y / log a

Övning 1

Ränta på ränta är en funktion som ökar exponentiellt. Om du sätter in 1000kr på en bank med årsränta på 6% hur många år tar det innan du är uppe i 5000kr?

Tips: slutsumman = insatt belopp $\cdot$ (1+räntan)^år

Lösning

Talet e

Talet $e$ är basen i det så kallade naturliga logaritmsystemet. Den naturliga logaritmen av e, ln(e) är 1 liksom tiologaritmen av 10 är 1. e har ett numeriskt värde på cirka 2.718281828 Talet e har den praktiska egenskapen att den är sin egen derivata. (Se Matematik C/Derivata)

Talet "e"

Talet "e" används vid derivering av exponentialfunktioner.

Vi utgår från den välkända formeln för exponentialfunktioner:

$y=C\cdot a^{x}$ (där "C" är skärningen med y-axeln och där "a" är den procentuella förändringen)

Om vi vill derivera denna formel, alltså beräkna lutningen (hastighetsförändringen) i en punkt på kurvan, börjar vi med att ställa upp derivatans definition:

$f^{\prime }(x)={\frac {f(x+h)-f(x)}{h}}$

"f'(x)" utläses "f prim x" och innebär derivatan i punkten x. För att kunna beräkna lutningen måste vi ha (precis som i en rät linje) två punkter. Därför inför vi detta där ena punkten med x-koordinaten "x" och som ger y-värdet "f(x)" samt en punkt med x-koordinaten "x+h" som ger y-värdet "f(x+h)". När vi sedan ska beräkna lutningen i en punkt, var som helst på kurvan, låter vi "h" närma sig 0 (noll), vilket ger oss lutningen i en punkt.

Nu kan vi fortsätta vårt bevis:

$f^{\prime }(x)={\frac {f(x+h)-f(x)}{h}}$

Vår funktion var $y=C*a^{x}\Rightarrow y^{\prime }={\frac {(C*a^{x+h})-(C*a^{x})}{h}}$

Vi förenklar detta uttryck genom att bryta ut, "C * a^x" och vi får:

y' = (C * a^x) * ((a^h - 1)/h)

Som vi kan se, har vi fått vårt ursprungliga uttryck åter igen, alltså "C * a^x".

För att göra denna derivering oerhört mycket lättare, låter vi ((a^h - 1)/h) vara lika med 1, eftersom detta ger en mycket lätt derivering.

Detta ger: ((a^h - 1)/h) = 1

           a^h - 1 = h
           a^h = h + 1
           a = (h + 1)^(1/h)

Låter vi nu "h" gå mot noll, vilket vi sade skulle genomföras för att fullborda derivering, får vi följande värden:

   h              a ---> (h + 1)^(1/h)

  0.1             2,593742...
  0.01            2,704813...
  0.001           2,716923...
  0.0001          2,718145...
  0.000001        2,718280...

Som vi kan se med denna tabell, verkar tydligen "a" närma sig talet ett tal som ungefär är 2,71828. Låt oss nu kalla detta tal för "e"

Vårat ursprungliga uttryck såg ut på följande vis: y = C * a^x

Om vi nu byter ut "a" till "e" så kan vi lätt derivera: $y=C*e^{x}y'=C*e^{x}$ (!!!)

Se även