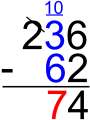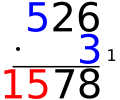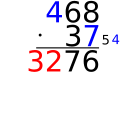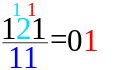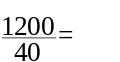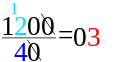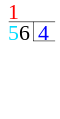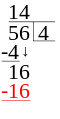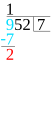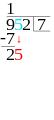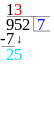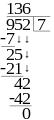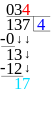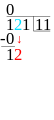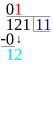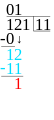Matematik för årskurs 7-9/Taluppfattning och räkning/Räkning/Heltalsräkning

Här tar vi upp hur man ställer upp och räknar med heltal. Heltal är alla sådana tal som vi vanligtvis räknar med. Till exempel: 'Det är 3 bananer i korgen'. Eller 'Vi fick 150 kr att handla för'.
Om talen vi behöver räkna med är för stora för att kunna räknas i huvudet behöver man ställa upp dem på något sätt. Beroende på vilka tal, vilket räknesätt och vad man själv gillar så finns det flera olika sätt att ställa upp. Här ska vi visa för de fyra grundläggande räknesätten: addition, subtraktion, multiplikation och division.
Addition
[redigera]
Addition är när man lägger ihop tal. Addition kallas i vardagligt tal för plus. Resultatet av en addition kallas summa. Vid addition spelar det aldrig någon roll i vilken ordning man adderar. Fem adderat med tio är till exempel samma sak som tio adderat med fem vilket kan skrivas som 5 + 10 = 10 + 5. Man kan helt enkelt ta addition i den ordning man tycker är lättast.
Det finns flera sätt ett ställa upp additioner som man inte klarar av att räkna i huvudet. Här beskrivs några olika sätt.
Uppställning
[redigera]Talen skrivs ovanför varandra så att entalsiffrorna hamnar ovanför varandra och tiotalsiffrorna ovanför varandra och så vidare. Därefter adderas alla ental. Entalet i svaret skrivs under entalen. Blir svaret tio eller mer skrivs tiotalssifran ovanför tiotalsiffrorna. Sedan adderas alla tiotalen. Även den som blev om det blev en från entalen. Svaret skrivs likadant.
|
Exempel | ||
|---|---|---|
|
|
Talsorter
[redigera]När man adderar med talsorter delar man upp talen i deras olika beståndsdelar och adderar ental för sig, tiotal för sig och hundratal för sig. Till sist lägger man ihop alltihop.
|
Exempel | ||
|---|---|---|
|
|
Kompensationsräkning
[redigera]Detta är en metod som kan användas när ett tal ligger nära något som är lätt att räkna med. Om man då minskar det ena talet och ökar det andra lika mycket kommer summan av talen inte ändra sig. Därför ändra man det ena till något som är lätträknat och så gör man tvärtom med det andra talet.
Om man exempelvis ska räkna ut 590 + 123 så är 590 ganska nära 600 som är ett lätträknat tal. Därför kan man öka 590 till 600 om vi samtidigt minskar 123 lika mycket.
Alltså blir 590 + 123 = 600 + 113 = 713
Givetvis kan man använda samma metod om ett tal är lite mer än något lätträknat också. Exempelvis i 705 + 113 som då blir 700 + 118 vilket lätt kan räknas ut till 818.
|
Exempel | ||
|---|---|---|
|
|
Övningsuppgifter
[redigera]|
Uppgifter | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
1. Beräkna
2. Beräkna
3. I en kiosk kostar en korv med bröd 20 kronor. En läsk kostar 15 kronor. Hur mycket kostar båda tillsammans?
4. Om du har tre tjugokronorssedlar och en femtiokronorssedel, hur mycket pengar har du då?
5. En tröja kostar 390 kronor. Ett par jeans kostar 750 kronor. Hur mycket kostar båda tillsammans?
6. Gå till Google. Sök efter 10 + 20. Vad får du för svar?
7. Vad händer om du skriver 100 + 50 i adressfältet på din webbläsare och trycker enter?
8. Använd miniräknare och lös följande uppgifter:
9. Vilka siffror saknas i följande uträkningar:
10. Beräkna
11. Beräkna
12. Om man har ett mynt och en sedel av varje valör, hur mycket pengar har man då? Mynt finns som 1 kr, 2 kr, 5 kr och 10 kr. Sedlar finns som 20 kr, 50 kr, 100 kr, 200 kr och 500 kr.
13. I en affär kostar ett par jeans som du vill ha 780 kr. När du är där ser du en snygg tröja som kostar 290 kronor. Hur mycket kostar båda plaggen tillsammans?
14. Ett hur är 120 kvadratmeter stort. Det har dessutom ett 60 kvadratmeter stort garage och ett uthus på 15 kvadratmeter. Hur stor är den sammanlagda ytan?
15. Googla efter 54+76.
16. Gå till http://www.wolframalpha.com/
17. Vilka siffror saknas i följande uträkningar:
Uppgifter om addition tillhör de grundläggande kunskaper som ni redan bör kunna i årskurs 7. Om ni vill räkna svårare uppgifter så kan ni kolla på fördjupningen eller så finns det svårare uppgifter i andra kapitel.
18. Beräkna summan av alla jämna tal från 0 till 100.
19. Beräkna summan av alla tal från:
20. I följande tal är en del av siffrorna utbytta mot bokstäver. Vilka siffror motsvarar bokstäverna?
|
Subtraktion
[redigera]
Subtraktion, eller minus som det också kallas, är motsatsen till addition. I stället för att lägga till så ska man nu dra ifrån.
Man ställer upp och räknar subtraktioner väldigt likt som man gör vid additioner.
Resultatet av en subtraktion kallas differens och är skillnaden mellan talen.
Uppställning
[redigera]På samma sätt som vid addition så ställer man upp ental över ental, tiotal över tiotal, hundratal över hundratal och så vidare.
Därefter räknar man ental för sig, tiotal för sig och hundratal för sig.
Det som nu är nytt är att det inte alltid går att subtrahera vilka tal från vilka hur som helst. Om man försäker subtrahera till exempel 7 från 2 så saknas det ju 5 för att det ska gå (om man inte räknar med negativa tal, men det kommer senare). Vad man då får göra är att växla. Om det exempelvis saknas ental för att man ska kunna subtrahera entalen så växlar man från tiotalen. Man kan säga att man växlar in en tiokrona för att få tio enkronor. Då går det att utföra subtraktionen!
Om man har växlat så är det viktigt att notera det så att man när man ska subtrahera nästa talsort vet om att man har växlat bort en och har en färre än man annars skulle haft. Detta brukar man notera genom att stryka över siffran man har växlat ifrån.
|
Exempel | ||
|---|---|---|
|
|
Kompensationsräkning
[redigera]På samma sätt som vid addition kan man också använda kompensationsräkning om ett tal ligger nära något lätträknat. Om man exempelvis ska räkna ut 571 – 103 så är 103 ganska nära 100 som är ett lätträknat tal. Vad vi då gör är att vi subtraherar 100 och sedan tar bort ytterligare 3. Detta kan man dock göra i valfri ordning. Antingen 571 – 100 = 471 och sedan 471 – 3 = 468 eller 571 – 3 = 568 och sedan 568 – 100 = 468.
Givetvis kan man också vid subtraktion använda samma metod om ett tal är lite mindre än något lätträknat också. Om vi exempelvis ska beräkna 705 – 96 så tar vi bort 100 och sedan lägger till 4. Även här kan man givetvis räkna i valfri ordning. Alltså: 705 – 100 = 605 och sedan 605 + 4 = 609 eller 705 + 4 = 709 och sedan 709 – 100 = 609.
Utfyllnadsalgoritmen
[redigera]Subtraktioner kan även räknas som additioner. Ett exempel på detta är utfyllnadsalgoritmen, då börjar man med det mindre talet och adderar tal till det tills det är lika stort som det större talet. Differensen blir då summan av de adderade talen. Detta görs fördelaktigt genom att ta en siffra i taget.
|
Exempel | ||
|---|---|---|
|
|
Övningsuppgifter
[redigera]|
Uppgifter | ||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
1. Beräkna
2. Om du har 250 kronor och skänker bort 100 kr, hur mycket har du sedan kvar?
3. En dator kostar 5400 kronor. Du har fått 1800 kr i rabatt. Hur mycket måste du betala?
4. Räkna på miniräknare:
5. En bankir var 47 år gammal och hade tre barn. En dag såg han 7 cyklister när han åkte till jobbet. På jobbet hade han 8 kollegor som jobbade på samma kontor men tre av kollegorna var sjuka och hade stannat hemma. Det var fyra kunder där. Hur många jobbade på kontoret den dagen?
6. Beräkna
7. Jan är 182 cm lång. Per är 17 cm kortare. Hur lång är Per?
8. Du har fått sommarjobb som diskare. En gång ska du diska 125 tallrikar. Efter en stund har du diskat 67 st. Hur många har du kvar att diska?
9. Googla efter 9000000000-900000000.
10. Varför är inte (15 − 10) − 5 samma sak som 15 − (10 − 5)?
11. Hur ska du göra för att räkna ut 9876543210 − 1234567890 med en vanlig miniräknare?
12. Vad är 8 000 000 000 000 − 5 000 000 000 000?
C-nivå och A-nivå Uppgifter om subtraktion tillhör de grundläggande kunskaper som ni redan bör kunna i årskurs 7. Om ni vill räkna svårare uppgifter så kan ni kolla på fördjupningen eller så finns det svårare uppgifter i andra kapitel. Fördjupning 13. Vad är 100 − 99 + 98 − 97 + … − 1 ?
14. I följande tal är en del av siffrorna utbytta mot bokstäver. Vilka siffror motsvarar bokstäverna?
|
Multiplikation
[redigera]
Multiplikation är vad som vanligtvis kallas gånger. När man multiplicerar tar man två eller flera faktorer och multiplicerar ihop dem till en produkt. Det man ska multiplicera kallas alltså för faktorer och svaret man får kallas för produkt. När man multiplicerar spelar det precis som vid addition aldrig någon roll i vilken ordning man multiplicerar. Till exempel är ju 3 st fyror 12, precis som 4 treor också är.
Multiplikation är samma sak som upprepad addition. T.ex. 3 ⋅ 2 = 3 + 3 = 2 + 2 + 2 = 6.
Multiplikation kan skrivas på två sätt, antingen med en liten prick eller med ett litet kryss ( ⋅ eller × ). På avancerad nivå så betyder ibland ⋅ och × olika saker. Det gäller till exempel om man räknar med något som heter matriser. Men detta spelar ingen roll för vanlig multiplikation så nu kan vi använda vilket vi vill. Eftersom × ibland ser så likt ut ett x så kommer vi här använda pricken. Sju multiplicerat med fem skriver vi alltså 7 ⋅ 5.
På datorer så används ofta en stjärna ( * ) för multiplikation. Det är den knappen som ligger till höger mellan ä- och enter-knappen. Den används för att det ibland är svårt att skriva rätt tecken. Om du till exempel ska googla efter en uträkning eller om du använder Excel ska du använda stjärnan.
Även multiplikation kan ställas upp på flera sätt. Här visar vi några bra sätt.
Uppställning
[redigera]Precis som med addition och subtraktion så skrivs talen ovanför varandra även om det inte här är lika noga att de olika talsorterna kommer över varandra. Det märks tydligare sedan när vi ska multiplicera decimaltal. Lättast är om man skriver det talet med färst antal siffror nederst.
Därefter börjar vi med den sista siffran (entalet) i det nedre talet och multiplicerar det med den sista siffran i det övre talet (entalet). Tiotalet i produkten som blir skrivs vid sidan av som en minnessiffra och entalet skrivs under. Därefter multipliceras det understa talets sista siffra med översta talets näst sista siffra. På denna produkt adderas minnessiffran. Tiotalet skrivs återigen vid sidan av och entalet till vänster om det förra entalet. Detta upprepas tills alla siffror i det övre talet är multiplicerade. Sedan gör man likadant med nästa siffra i det undre talet fast här skrivs alla tal ett steg längre åt vänster. Detta eftersom vi nu håller på med det undre talets tiotal som är en position längre åt vänster än entalen vi innan multiplicerade.
Sedan gör man likadant med alla siffror i det undre talet med varje ny siffras produkt ett steg längre åt vänster.
Nollor som är i slutet av talen när man multiplicerar kan man hoppa över och flytta direkt till svaret!
Om ett eller båda av talen man ska multiplicera slutar på noll kan man hoppa över alla de nollorna och lägga till dem efteråt eller så kan man göra som i exemplet nedan, att man skriver nollorna vid sidan av. Eftersom noll multiplicerat med vilket tal som hellst alltid blir noll behöver man ju inte göra de multiplikationerna. Man kan också tänka att till exempel talet 430 är 43 ⋅ 10. När man då multiplicerar med 430 börjar man med att multiplicera med 43. När man har gjort det så skulle man också multiplicera med 10 och då läggs det ju bara på en nolla i slutet.
Om man ska räkna på tal där båda slutar med nollor kan man på samma sätt hoppa över nollorna i båda talen och räkna som om de inte fanns och efteråt lägga på båda talens nollor på svaret. Om man exempelvis ska beräkna 700 ⋅ 3000 så kan man räkna 7 &sdot 3 som är 21 och sedan lägga på sammanlagt 5 nollor så att svaret blir 2100000.
|
Exempel | ||
|---|---|---|
|
|
Rita streck
[redigera]Multiplikation kan också beräknas genom att endast rita streck och räkna hur många ställen strecken korsar varandra. Man ritar strecken i grupper med en grupp streck för entalen och en grupp för tiotalen och så vidare. 24 ritas alltså med fyra streck i en grupp till höger och sedan två streck i en grupp till vänster om dem.
Om man har två tal som ska multipliceras ritas strecken lite snett åt var sitt håll så att de kan korsa varandra som du kan se i exemplet.
Nu är det bara att räkna hur många korsningar vi har. Man börjar längst till höger där vi har entalen. Nästa kolumn åt vänster där det finns två ställen med korsningar är tiotalen. Sedan hundratalen och sedan tusentalen och så vidare.
Bevis
[redigera]
Man kan bevisa att denna metod fungerar på två olika sätt. Antingen så jämför man med hur den vanliga uppställningen går till för då kan man se att det faktiskt är samma beräkningar man genomför. Den andra metoden kan kräva att ni först har koll på lite om räkneregler. För att visa hur detta fungerar behöver man först dela upp talen i sina olika talsorter, ental för sig, tiotal för sig och så vidare, precis som man gör när man ritar strecken.
123 Blir då 100 + 20 + 3. 100 kan skrivas som 1 ⋅ 100 och 20 kan skrivas som 2 ⋅ 10. Då kan hela talet skrivas som 1 ⋅ 100 + 2 ⋅ 10 + 3. Om man gör likadant med 45 blir det 4 ⋅ 10 + 5. När dessa två tal ska multipliceras ihop så får vi:
- (1 ⋅ 100 + 2 ⋅ 10 + 3) ⋅ (4 ⋅ 10 + 5)
När sådana parenteser ska multipliceras med varandra så ska allt i den ena parentesen multipliceras med allt i den andra. Då får vi:
- 1 ⋅ 100 ⋅ 4 ⋅ 10 + 1 ⋅ 100 ⋅ 5 + 2 ⋅ 10 ⋅ 4 ⋅ 10 + 2 ⋅ 10 ⋅ 5 + 3 ⋅ 4 ⋅ 10 + 3 ⋅ 5
Eftersom man får multiplicera i vilken ordning man vill kan det skrivas om som:
- 1 ⋅ 4 ⋅ 100 ⋅ 10 + 1 ⋅ 5 ⋅ 100 + 2 ⋅ 4 ⋅ 10 ⋅ 10 + 2 ⋅ 5 ⋅ 10 + 3 ⋅ 4 ⋅ 10 + 3 ⋅ 5
Vilket är samma som:
- 1 ⋅ 4 ⋅ 1000 + 1 ⋅ 5 ⋅ 100 + 2 ⋅ 4 ⋅ 100 + 2 ⋅ 5 ⋅ 10 + 3 ⋅ 4 ⋅ 10 + 3 ⋅ 5
Nu kan vi se att ental multiplicerat med ental blev ental eftersom där inte finns med något ⋅ 10 eller ⋅ 100 eller ⋅ 1000. på nästa plats har vi två med tiotal, precis som det blir när man ritar strecken och två med hundratal och en med tusental.
Uppdelning
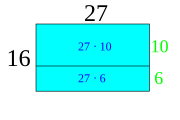
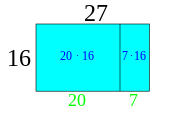
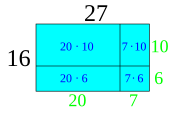
[redigera]Eftersom att multiplikation är upprepad addition så är t.ex. 3 ⋅ 12 = 3 ⋅ 10 + 3 ⋅ 2. På liknande sätt kan man dela upp andra multiplikationer så att en komplicerad multiplikation blir många lätta.
Man kan illustrera detta genom att rita rektanglar. Om en rektangel är 27 bred och 16 hög så har den en area av 27 ⋅ 16. I stället för att räkna ut 27 ⋅ 16 kan vi lika gärna räkna ut 27 ⋅ 10 + 27 ⋅ 6 eller 20 ⋅ 16 + 7 ⋅ 16 eller 20 ⋅ 10 + 7 ⋅ 10 + 20 ⋅ 6 + 7 ⋅ 6. Det är bara att välja det som man tycker är lättast.
-
Arean av rektangeln är 16 ⋅ 27
-
Arean kan delas upp i två rutor som tillsammans är lika stora som hela rutan
-
Arean kan lika gärna delas upp åt detta hållet
-
Arean kan också delas upp i flera rutor
Här följer några olika exempel där vi har delat upp komplicerade multiplikationer och räknat de i många lätta multiplikationer.
|
Exempel | ||
|---|---|---|
|
|
Kompensationsräkning
[redigera]På samma sätt som vid addition kan man ibland stöta på multiplikationer som är svåra men där det finns tal nära som är mycket lättare att räkna. Till exempel är 97 ⋅ 99 ganska krångligt att ställa upp. 97 ⋅ 100 är mycket lättare så vi räknar ut det istället vilket blir 9700. Men vi skulle ju bara multiplicera med 99 och inte med 100 så svaret är en 97:a för högt. Om vi tar bort 97 så att vi får 9603 så är det 99 ⋅ 97.
Detta kan man också utnyttja om ett tal är lite för högt som om man ska beräkna 102 ⋅ 65. Då kan man rräkna ut 100 ⋅ 65 istället. Det blir 6500. Denna gången saknas det två 65:or så då lägger vi till dem (2 ⋅ 65 = 130) och får 6630.
Matematiskt så skrivs detta:
97 ⋅ 99 = 97 ⋅ (100 − 1) = 97 ⋅ 100 − 97 ⋅ 1 = 9700 − 97 = 9603
102 ⋅ 65 = (100 + 2) ⋅ 65 = 100 ⋅ 65 + 2 ⋅ 65 = 6500 + 130 = 6630
Övningsuppgifter
[redigera]|
Uppgifter | ||||
|---|---|---|---|---|
|
1. Beräkna
2. Beräkna
3. Beräkna
4. Beräkna
5. Area på fyrkanter beräknas genom att man multiplicerar längden på de två sidorna. En rektangel är 11 cm lång och 5 cm bred. Vad har den för area? 6. En dag är Jens väldigt sugen på glass. Glassarna kostar 15 kr/st. Jens köper 7 st. Hur mycket får Jens betala? 7. Beräkna med miniräknare:
8. Vad blir mest, 2 ⋅ 5 ⋅ 2 ⋅ 5 ⋅ 2 ⋅ 5 eller 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3?
9. Beräkna
10. Beräkna
11. Beräkna
12. Beräkna
13. En fotbollsplan är 68 meter bred och 105 meter lång. Hur stor area har den? Arean beräknas genom att multiplicera längd och bredd. 14. Hur mycket skiljer det på 99 ⋅ 101 och 100 ⋅ 100? 15. I en affär hade de en dag 180 kunder. I genomsnitt tjänade affären 75 kronor per kund. Hur mycket tjänade affären den dagen? 16. I fysiken kan man räkna energi för en maskin som hur mycket effekt maskinen har gånger hur många sekunder maskinen var igång. En lampa som är på 60 watt som lyser i en minut, hur mycket energi blir det? 17. Hur många sekunder är det på ett dygn? 18. Vilken blir sista siffran om du multiplicerar 100 stycken 5:or? 19. Ungefär hur många löv är det på ett träd? Tänk dig hur många stora grenar det är. Multiplicera med hur många mellanstora grenar det är på varje stor gren. Multiplicera sedan med hur många små grenar det är på varje mellanstor gren. Multiplicera sist med hur många löv det är på varje liten gren.
Uppgifter om subtraktion tillhör de grundläggande kunskaper som ni redan bör kunna i årskurs 7. Om ni vill räkna svårare uppgifter så kan ni kolla på fördjupningen eller så finns det svårare uppgifter i andra kapitel. Fördjupning 20. Tänk dig att vi multiplicerar alla tal från 1 till 100.
21. I följande tal är en del av siffrorna utbytta mot bokstäver. Vilka siffror motsvarar bokstäverna?
|
Division
[redigera]
Division är vad som vi menar när vi säger att vi ska dela. Division är det som hjälper oss när vi vill svara på frågor i stil med hur många glassar kan jag köpa för 150 kr eller hur många varv snurrar ett cykelhjul på 1 km? Division kan sägas vara motsatsen till multiplikation på samma sätt som subtraktion är motsatsen till addition.
I division spelar ordningen stor roll när man ställer upp. Det är ju stor skillnad på att fråga: hur många A4-papper får plats på en fotbollsplan (jättemånga) och hur många fotbollsplaner får plats på ett A4-papper (bara en liten pyttebit av en). Talet som vi ska dela upp kallas täljare och talet vi ska dela med kallas nämnare. Svaret kallas kvot. Som minnesreegel vid kort division (se nedan) så står täljaren i taket, och nämnaren där nere.
För att räkna ut en division med papper och penna kan man använda flera olika metoder även om alla bygger på samma matematiska principer. Testa gärna själv att ställa upp samma tal med olika metoder och se likheterna.
Ibland vill man utföra divisioner med stora tal. Exempelvis om vill veta hur många tusenlappar man har om man har 4000 kr. Divisionen vi vill utföra är då 4000 / 1000. Vad vi då kan göra är att förkorta den divisionen. (Mer om förkortningar kommer i kapitlet om bråk.) Istället för att dela upp 4000 i tusen olika delar tar vi tusen i taget av 4000. då blir divisionen istället 4 / 1 som är jättelätt. Om vi tar tusen i taget från 4000 blir det altså 4. Vad vi har gjort är att vi har strukit nollor från både täljaren och nämnaren i divisionen. I vårat exempel strök vi 3 st från båda. I alla divisioner får man alltid stryka nollor, så många man vill, så länge som man stryker lika många från både täljaren som nämnaren.
Kort division
[redigera]Kort division är det vanligaste sättet att ställa upp en division. Det är också, som man hör på namnet, kort och tar inte så mycket plats.
Vad man gör är att man skriver täljaren över divisionsstrecket (ett vanligt streck) och nämnaren under. Täljaren är det talet som ska delas upp och nämnaren är det talet som säger i hur stora eller hur många delar. Så om man vill veta hur många 4:or som får plats i 56 så skriver man 56 över divisionsstrecket och 4:an under.
Sedan kollar man hur många av nämnaren som det får plats i täljarens första siffra och skriver det svaret till höger. Om det blir en rest skriver man resten vid täljarens nästa siffra. Därefter kollar man likadant med nästa siffra fast med resten som tiotalsiffra och skriver det svaret till höger om det förra svaret. Så håller man på till siffrorna är slut.
Blir det en rest kvar i slutet så kan man göra på lite olika sätt. I kapitlet om decimaltal går vi igenom hur man gör för att räkna ut decimalerna och i bråkkapitlet går vi igenom hur man gör för att skriva resten som bråk. Nu nöjer vi oss med att skriva att det blev en rest.
|
Exempel | ||
|---|---|---|
|
|
Liggande stolen
[redigera]
Liggande stolen är, precis som kort division, en metod för att utföra en division med papper och penna. Den är även användbar för polynomdivision inom algebran vilket kommer senare på gymnasiets matematik.
Liggande stolen tar mer plats än kort division och utförs noggrannare även om det egentligen är precis samma beräkningar som utförs. Vid polynomdivision (som kommer på gymnasiet) så är det dock väldigt svårt att beräkna resterna i huvudet, så där används denna metoden istället.
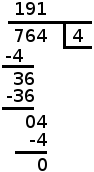
Till höger finns ett exempel där 764 skall divideras med 4 med hjälp av liggande stolen. Det går till på följande vis:
- Vi börjar med att fokusera täljarens första siffra (i det här fallet siffran 7) och se hur många gånger vi kan dela den jämnt med nämnaren (som är 4). 7 delat på 4 blir 1, och denna kvot antecknas på kvotraden rakt över täljarsiffran.
- Divisionen ger också en rest som vi måste räkna ut och sedan ta hand om. Därför får vi multiplicera den just beräknade kvoten (1) med nämnaren (4) igen och anteckna produkten (som blir 4) rakt under vår täljarsiffra.
- Nu kan vi subtrahera denna produkt (4) från den fokuserade täljarsiffran (7) och anteckna resten (3) rakt under. Detta är alltså vad som blev över när vi påstod att 7 delat på 4 bara blir 1, och denna rest får vi ta med oss när vi övergår till att räkna på täljarens nästa siffra.
De tre stegen som beskrivits ovan utgör hela algoritmen. Varje siffra i täljaren ska vi bearbeta på samma sätt, och varje gång det blir en rest, tar vi med oss den till nästa beräkningsrunda. Här kommer runda 2:
- Vi ska nu arbeta med täljarens andra siffra (6). Skriv den direkt efter förra rundans rest (3). Det ger 36 som är den del av täljaren som vi nu ska räkna på. Dela den med nämnaren (4). Det går faktiskt jämnt ut, och kvoten blir 9. Anteckna den på kvotraden rakt över täljarsiffran.
- Nu är det dags att multiplicera kvoten (9) med nämnaren (4) och anteckna produkten (36) rakt under den del av täljaren (36) som vi nu har fokus på.
- Subtrahera sedan produkten (36). Här blir resten 0. Det visste vi redan, eftersom vi märkte att divisionen 36 / 4 gick jämnt ut.
Tredje och i det här fallet sista rundan görs på samma sätt:
- Flytta ner sista täljarsiffran (4) till resten (0). Det blir 04. Dela 04 på 4 och skriv kvoten (1) på kvotraden.
- Multiplicera kvoten (1) med nämnaren (4). Det blir 4 som skrivs rakt under den täljarsiffra som vi fokuserar.
- Subtrahera 4 från 4 och skriv resten (0) längst ner.
Vi har nu bearbetat alla siffrorna i täljaren och sista beräkningsrundan gav ingen rest. Hela divisionen gick alltså jämnt upp och vi kom fram till att 764 / 4 = 191. Om divisionen inte hade gått jämt ut hade vi precis som vid kort division fått skriva resten vid sidan av.
|
Exempel | ||
|---|---|---|
|
|
Trappan
[redigera]-
Liggande stolen
-
Trappan
Trappan och liggande stolen är exakt samma uppställning förutom var man sätter ut nämnaren. I liggande stolen sätter man nämnaren i en ruta till höger medan man i trappan sätter den till vänster. Som ni kan se i exemplet nedan är det sedan exakt samma räkningar förutom just nämnaren. Anledningen att trappan och liggande stolen båda finns är historiska. Skolöverstyrelsen som var den myndighet som förr bestämnde hur skolorna skulle undervisa bestämnde innan 1979 att man skulle ställa upp division med trappan och efter 1979 sa de i stället att man skulle använda liggande stolen. Sedan 1994 får man använda vilken man vill i skolorna.
|
Exempel |
|---|
|
|
Övningsuppgifter
[redigera]|
Uppgifter |
|---|
|
1. Beräkna
2. Du har fått 60 kronor att köpa godis för till dig och dina två kompisar. Eftersom ni inte kan komma överens om vad för sorts godis ni vill ha delar ni upp pengarna. Hur mycket pengar får ni var?
2. Beräkna
3. Beräkna
C-nivå och A-nivå Uppgifter om division tillhör de grundläggande kunskaper som ni redan bör kunna i årskurs 7. Om ni vill räkna svårare uppgifter så kan ni kolla på fördjupningen eller så finns det svårare uppgifter i andra kapitel. Fördjupning 4. Vilket tal ska delas med 15 för att få 15? 5. Hur många jordklot behöver man lägga bredvid varandra för att det ska bli lika långt som det är rakt igenom solen? 6. Man kan utan att utföra hela divisionen säga om det blir en rest eller inte när man delar med 2, 3, 4, 5, 6, 9 och 10. Hur? |
Blandat
[redigera]På samma sätt som addition och subtraktion är varandras motsatser är multiplikation och division varandras motsatser. När man adderar eller subtraherar händer ingenting om man adderar eller subtraherar noll och när man multiplicerar eller dividerar händer ingenting om man multiplicerar eller dividerar med ett.
När man multiplicerar kan man strunta i alla nollor på slutet och lägga till dem på svaret sist. När man dividerar kan man stryka nollor i både täljare och nämnare, så länge som man stryker lika många på båda ställena.
Övningsuppgifter
[redigera]- Mer övningsuppgifter: Blandade uppgifter.
Länkar
[redigera]Fler digitala matteböcker med genomgångar om vanlig räkning:
Mer (avancerad) information om räkesätten finns också på wikipedia:
Teacher on demand (videogenomgångar):
Dataspel där man ska räkna olika tal så fort som möjligt.