Fria matteboken: matematik 2b/Korrelation, samband, funktioner och funktionsanpassning/Uppgifter
Samband, korrelation och kausalitet
[redigera]Förklara begrepp
[redigera]Läs igenom och försök förbättra förklaringarna av de här begreppen. (Om något begrepp saknas kan du påbörja en beskrivning!)
Viktiga begrepp
Övriga begrepp
Klassa korrelationer
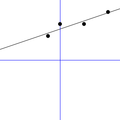
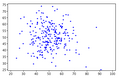
[redigera]För varje diagram nedan:
- Finns det en stark, svag, eller ingen korrelation?
- Om det finns en korrelation, är den positiv eller negativ?
- Vilka korrelationer är de mest osäkra?
Jämför dina svar med bänkgrannens, eller skriv ner dem på papper.
-
Diagram 1
-
Diagram 2
-
Diagram 3
-
Diagram 4
-
Diagram 5
-
Diagram 6
-
Diagram 7
-
Diagram 8
-
Diagram 9
-
Diagram 10
-
Diagram 11
-
Diagram 12
-
Diagram 13
-
Diagram 14
-
Diagram 15
-
Diagram 16
Nyfiken på korrelationer
[redigera]En korrelation berättar om det finns ett samband mellan två uppsättningar av data, men inte vad sambandet beror på. Skriv ner någon korrelation som du tror finns, och skulle vilja se ett diagram över. Skriv också ner om du tror att korrelationen är positiv/negativ, och om den är stark/svag.
- Jag undrar om det finns en korrelation mellan att vara duktig på musik och duktig på matematik. Jag tror att det finns en svag positiv korrelation.
- Jag undrar om det finns en korrelation mellan hur stor risk man har för hjärtinfarkt och hur mycket vegetarisk man man äter. Jag tror att det finns en stark negativ korrelation.
- Jag undrar om det finns en korrelation mellan hur mycket choklad man äter och hur mycket finnar man får. Jag tror att det inte finns någon korrelation.
- Jag undrar om det finns en korrelation mellan hur ofta man blir sjuk och hur hygieniskt man lever. Jag tror att det finns en stark negativ korrelation.
- Jag undrar om det finns en korrelation mellan hur mycket hårdrock man lyssnar på och hur snäll man är. Jag tror att det finns en svag positiv korrelation.
- Jag undrar om det finns en korrelation mellan hur mycket datorspel man spelar och hur våldsam man är. Jag tror att det inte finns en korrelation (eller kanske en mycket svag positiv korrelation).
- Jag undrar om det finns en korrelation mellan hur mycket solarium man solar och att få hudcancer. Jag tror att det finns en mellanstark positiv korrelation.
- …
Hitta korrelationer på gapminder.org
[redigera]Gå till gapminder.org och klicka fram ett antal diagram för olika data. Välj ut ett diagram som du tycker är intressant, och beskriv det enligt följande mall:
- Diagrammet på (länk till Gapminder) beskriver förväntad livslängd (y-axel) och fattigdom (x-axel). Det är en medelstark negativ korrelation. En möjlig förklaring till korrelationen är… En annan möjlig förklaring är…
Lägg in beskrivningen som en ny punkt här nedan. (Här finns en video som förklarar hur du använder Gapminder.) (Här finns även en till video som förklarar gapminder: http://www.youtube.com/watch?v=M8uz2Qt7F5g)
- …
- …
| Gapminder skapades av svensken Hans Rosling, för att göra det lättare att jämföra data för olika länder i världen. Med hjälp av Gapminder kan man exempelvis se hur stor andel av ett lands befolkning som är analfabeter, hur många som röker, vad medellivslängden är, hur gamla kvinnor i genomsnitt är när de får sitt första barn, och en rad annan data. Man kan också se hur dessa data ändrats över tid, och – inte minst – kan man ställa dessa data mot varandra för att se om det finns någon korrelation mellan dem. År 2007 såldes mjukvaran bakom Gapminder till Google, och den fortsätter att utvecklas och användas. |
Regressionsanalys och matematiska modeller
[redigera]Förklara begrepp
[redigera]Läs igenom och försök förbättra förklaringarna av de här begreppen. (Om något begrepp saknas kan du påbörja en beskrivning!)
Viktiga begrepp
Formulera samband med funktioner
[redigera]Exempeluppgift
[redigera]På gapminder kan man se att förväntad livslängd i ett land är korrelerat med hur många barn kvinnor föder i genomsnitt. Då är det rimligt att modellera förväntad livslängd som en funktion av antal barn per kvinna.
L(b): Förväntad livslängd i ett land b: Antal barn varje kvinna föder, i genomsnitt
- Beskriv i ord vad det betyder att L(2,1) = 74. Svar: I ett land där kvinnor i genomsnitt föder 2,1 barn är den förväntade livslängden 74 år (enligt modellen).
- Enligt modellen skulle ett land där kvinnor i genomsnitt föder 1,9 barn ha en förväntad livslängd på 76 år. Hur skriver du det sambandet med funktionsnotation? Svar: L(1,9) = 76
- Ett land som har förväntad livslängd på 61 år borde, enligt vår modell, ha 4,6 barn per kvinna. Hur skriver du det sambandet med funktionsnotation? Svar: L(4,6) = 61
- Skriv ett uttryck för den förväntade livslängden för ett land där kvinnor i genomsnitt föder 3,2 barn. Svar: L(3,2)
- I Sverige är medellivslängden 81 år (2011). Beskriv i ord vad sambandet L(b1) = 81 betyder. Svar: I ett land där kvinnor i genomsnitt föder b1 barn är förväntade livslängden 81 år (enligt vår modell).
- Lägsta förväntade livslängden är 44 år och i Sierra Leone (år 2011). Beskriv i ord vad sambandet L(b2) = 44 betyder. Svar: I ett land där kvinnor i genomsnitt föder b2 barn är förväntade livslängden 44 år (enligt vår modell).
1: Barnadödlighet
[redigera]På gapminder.org kan man se att barnadödlighet i ett land är rätt starkt korrelerat med hur många barn varje kvinna föder i genomsnitt. Då är det rimligt att modellera barnadödligheten som en funktion av antal barn per kvinna:
d(b): Barnadödlighet i ett land (barn som dör innan 5 års ålder, per 1000 födda) b: Antal födda barn per kvinna, i genomsnitt
- Beskriv i ord vad det betyder att d(4,6) = 91.
- Enligt modellen skulle ett land där kvinnor i genomsnitt föder 1,9 barn ha en barnadödlighet på 25 av 1000. Hur skriver du det sambandet med funktionsnotation?
- Ett land som har barnadödlighet på 78 per 1000 födda borde, enligt vår modell, ha 3,6 barn per kvinna. Hur skriver du det sambandet med funktionsnotation?
- I Sverige är barnadödligheten 3 per 1000 födda barn. Beskriv i ord vad sambandet d(b1) = 3 betyder.
- Högsta rapporterade barnadödligheten är i Sierra Leone, med 200 per 1000 barn som dör innan de fyller 5 år. Beskriv i ord vad sambandet d(b2) = 200 betyder.
2: Usain Bolt
[redigera]Utgå från följande samband.
s(t): Antal meter Usain Bolt sprungit. t: Antal sekunder sedan startskottet.
- Vad betyder det att s(9,58) = 100?
- Efter 5 sekunder har Usain sprungit 42 meter. Hur skriver du det sambandet med funktionsnotation?
- Vad är s(0)?
- Rita en graf för hur du tror att s(t) kan se ut (för t mellan 0 och 9,58). Glöm inte att sätta ut vad axlarna står för.
- Lös ekvationen s(t1) = 90 med hjälp av din graf.
3: Färdigpizza
[redigera]Magister Falk har en mozarellapizza i frysen. På förpackningen står det att man ska grädda den i 250°C i 10 minuter. Då har pizzan blivit ungefär 100°C varm. I frysen är det -18°C.
T(t): Pizzans temperatur, i °C. t: Antal minuter sedan pizzan sattes in i ugnen.
- Vad är T(0)?
- Vad är T(10)?
- Vad betyder sambandet T(t1) = 0, uttryckt i ord?
- Rita en graf för hur du tror att T(t) kan se ut, mellan t=0 och t=10. Glöm inte att skriva vad som syns på respektive axel.
- Lös ekvationen T(t1) = 0 med hjälp av din graf.
| Om du försöker läsa den här uppgiften högt märker du att det är knepigt att ha stort T för temperatur samtidigt som man har litet t för tid. De variablerna används här ändå, eftersom det är de som brukar användas för att beteckna temperatur och tid. |
4: Lärarlöner
[redigera]År 2011 kunde lärarnas löner på skolan X uppskattas med den här funktionen:
L(Å): Förväntad månadslön, i kr Å: Lärarens ålder, i år
- Beskriv i ord vad sambandet L(40)=29600 betyder.
- Skriv upp ett uttryck för förväntad lön för en lärare som är 50 år.
- Skriv upp en ekvation som kan användas för att ta reda på när den förväntade lönen är 32000 kr.
- Beskriv i ord vad Å1 står för, i sambandet L(Å1)=30000.
- Beskriv i ord vad Å2 står för, i sambandet L(Å1)=35000.
| I verkligheten är L(Å) = 170Å + 22800. Kan du räkna ut vad Å1 och Å2 blir? |
Använda funktioner på grafritande räknare
[redigera]1: Lösa en ekvation grafiskt, steg för steg
[redigera]I den här uppgiften kommer vi att lösa ekvationen grafiskt, med hjälp av grafritande räknare. Vi kommer att göra det genom att rita upp en graf över vänsterledets värden för olika x-värden, och en annan graf för högerledets värden. Sedan kommer vi att ta reda på när de har samma värde, och vänsterledet alltså är lika med högerledet.
- Mata in funktionen Y1 = x3 – 3x i din räknare.
- Gör en värdetabell för funktionen, i intervallet -3 ≤ x ≤ 3.
- Vad är högsta och minsta funktionsvärdet i det här intervallet? Vad är högsta och minsta x-värdena?
- Ställ in Window-värdena i din räknare för att passa mot dessa x- och y-värdedn.
- Gör en graf över Y1.
- Mata in funktionen Y2 = x2 – 2 i din räknare.
- Titta på värdetabellen för funktionen i intervallet -3 ≤ x ≤ 3, och se var högsta och lägsta funktionsvärdet är.
- Ändra YMin och YMax i Window-inställningarna, om det behövs för att funktionen ska få plats.
- Rita upp en graf för Y2, tillsammans med Y1.
- Hur många skärningspunkter har graferna?
- Använd räknarens Intersect-funktion (under Calc) för att hitta skärningspunkterna. Vad är koordinaterna för skärningspunkterna?
- Vad är lösningarna till ekvationen ?
2: Undersöka extrempunkter och nollpunkter
[redigera]I den här uppgiften kommer vi att utforska hur funktionen f(x) = x3 – 3x beter sig.
- Mata in funktionen Y1 = x3 – 3x i din räknare.
- Gör en värdetabell för funktionen, i intervallet -3 ≤ x ≤ 3.
- Vad är högsta och minsta funktionsvärdet i det här intervallet? Vad är högsta och minsta x-värdena?
- Ställ in Window-värdena i din räknare för att passa mot dessa x- och y-värdedn.
- Gör en graf över Y1.
- Hur många nollställen har funktionen (i det här intervallet)?
- Vad är nollställena? (Tips: Använd root eller zero (under Calc) på din räknare.)
- Hur många extrempunkter har funktionen (i det här intervallet)?
- Vad är koordinaterna för extrempunkterna? (Tips: Använd max eller min (under Calc) på din räknare.)
3: Lösa en ekvation grafiskt
[redigera]I den här uppgiften kommer vi att lösa ekvationen grafiskt. Det är en av många ekvationer som inte går att lösa exakt, utan måste lösas grafiskt (eller med någon annan så kallad numerisk metod).
- Rita upp grafen för xx i intervallet -1 ≤ x ≤ 3. Se till att du har lämpliga värden för graffönstret.
- Rita upp grafen för 2x. Justera värdena för graffönstret om det behövs.
- Hur många skärningspunkter finns det mellan funktionerna, och var finns de?
- Vad är lösningen till ekvationen?
4: Lösa ekvationer grafiskt
[redigera]Välj en eller flera av dessa ekvationer, och lös dem grafiskt. Du kommer att behöva uppskatta själv om du hittat alla skärningspunkter. För vissa ekvationer kanske det inte finns några skärningspunkter – och då saknar ekvationen lösning.