Tävlingsprogrammering/Uppgifter/Flygbolaget

Flygbolaget

Bo Arding har startat ett flygbolag. Han har en tabell som visar hur lång tid det tar att flyga mellan olika flygplatser, och han har redan skapat en tidtabell för vilka sträckor bolaget ska trafikera och när flighterna (turerna ska avgå). Nu återstår bara en detalj: att köpa flygplan. Till sin förvåning upptäcker han att det är ganska dyrt med flygplan, så han vill inte köpa fler än nödvändigt. Skriv ett program som hjälper Bo att beräkna det minsta antalet flygplan som behövs för att flyga alla flighter (turer) i tidtabellen.

Vi tittar på alla fighter som avgår under ett dygn. Du kan anta att flygplanen befinner sig på vilka flygplatser du vill när dygnet börjar. Alla flygtider inkluderar in- och avlastning så en ny flight kan avgå vid samma tidpunkt som en annan anländer och ändå använda samma flygplan.

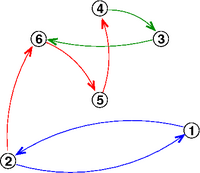
Flighterna i exemplet färgade enligt en tänkbar uppdelning: ett flygplan kan köra de röda, ett kan köra de blåa och ett kan köra de gröna flighterna. I allmänhet kan det gå flera flighter mellan två flygplatser.

Indata

På första raden står två heltal: antalet flygplatser (2 ≤ N ≤ 100) och antal flighter (turer) under dagen (1 ≤ M ≤ 500). Sedan följer N rader med N heltal på varje rad: en "avståndstabell" där det j:te talet på den i:te raden (Dij) anger hur många minuter det tar att flyga från flygplats i till flygplats j. Samma sträcka kan ta olika tid i olika riktningar, men tar alltid minst en minut. Talen på diagonalen är alltid 0 och varje triplett (i,j,k) av flygplatser uppfyller triangelolikheten, d.v.s. D_ij + D_jk ≥ D_ik. Slutligen följer M rader som beskriver flighterna. Varje rad består av tre heltal A, B och T, som anger att en flight ska gå från flygplats A till flygplats B vid tidpunkten T, räknat i minuter från midnatt (1 ≤ A,B ≤ N och 1 ≤ T ≤ 1440, d.v.s. ett dygn).

Utdata

En rad med ett heltal, det minimala antalet flygplan som behövs för att genomföra de planerade flighterna.

Exempel: Indata

6 7
0 150 50 110 45 120
145 0 180 90 60 80
50 160 0 40 38 45
110 90 37 0 50 20
47 60 40 52 0 65
120 80 40 20 60 0
1 2 170
6 5 400
5 4 470
2 6 318
4 3 520
3 6 700
2 1 25

Exempel: Utdata

Lösning[redigera]

Här gäller det att inse att om det kommit in ett flygplan till en flygplats så ska det skickas iväg på första möjliga flight därifrån. Det kan aldrig vara bättre att "spara" ett plan till nästa flight för då måste man ju ta ett "nytt" plan istället, d.v.s. en garanterad utgift. Detta är alltså ett exempel där en girig (greedy) algoritm fungerar.

I praktiken behöver man inte ens simulera förloppet, det räcker att para ihop de ankommande flygplanen med första bästa avgående flight. Om det går att göra nm sådana par, så behövs det M-nm flygplan.

Lösning i C:

#include <stdio.h>
#define MAXN 1000
#define MAXF 1000
 
int main() {
  int N,M,i,j,nm,bra,d[MAXN][MAXN], from[MAXF],to[MAXF],dep[MAXF],taken[MAXF];
  scanf("%d %d", &N,&M);
  for(i=0;i<N;i++) for(j=0;j<N;j++) scanf("%d", &d[i][j]);
  for(i=0;i<M;i++) {
    scanf("%d %d %d", &from[i], &to[i], &dep[i]); from[i]--; to[i]--;
    taken[i]=0;
  }
  nm=0;
  for(i=0;i<M;i++) {   //Loopa över de ankommande flighterna
    bra=-1;
    for(j=0;j<M;j++) if(i!=j && !taken[j]) {      //Loopa över de avgående flighterna
      if(to[i]==from[j] && dep[i]+d[from[i]][to[i]]<=dep[j] && (bra==-1 || dep[j]<dep[bra])) 
        bra=j;   //Om den passar och är den hittills tidigaste funna flighten så spara den i bra
    }
    if(bra!=-1) {
      nm++;           //Ännu en matchning hittad
      taken[bra]=1;     //Markera den avgående flighten som tagen så den inte kan användas igen
    }
  }
  printf("%d\n", M-nm);
  return 0;
}