Tävlingsprogrammering/Uppgifter/Brandlarmet

Brandlarmet

Brandlarmet går och du måste ta dig ut så fort som möjligt. Du befinner dig i en byggnad med ett antal utrymmen förbundna med dörrar. Varje utrymme kan klassas som "inomhus" eller "utomhus", och du behöver alltså bara ta dig till ett utrymme som räknas som utomhus. Men vissa dörrar är låsta och nyckeln finns bara i ett visst rum. Det är samma nyckel till alla låsta dörrar.

Det kan alltså ibland vara bättre att först springa och hämta nyckeln så att du sedan kan använda även de låsta dörrarna. Vilket som är det bästa sättet beror förstås på byggnadens utseende. Skriv ett program som, givet en karta över byggnaden, beräknar det minsta antalet sekunder du behöver för att ta dig ut.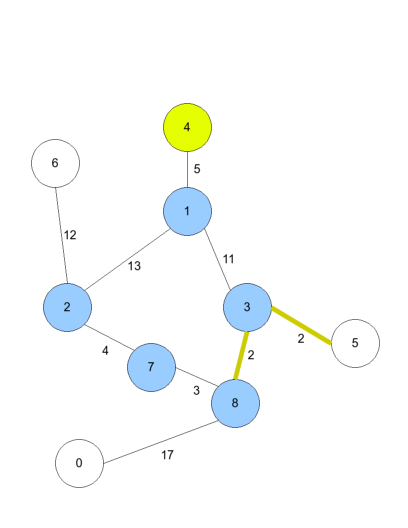

Figuren visar byggnaden i exemplet. Du befinner dig i utrymme 1. De vita ringarna är utomhus, den gula är utrymmet med nyckeln. Talet vid varje förbindelse anger tiden för att springa där, och de gula förbindelserna är låsta. Det snabbaste sättet att ta sig ut är 1 -> 4 -> 1 -> 3 -> 5, vilket tar 5+5+11+2=23 sekunder.

Indata

På första raden står antalet utrymmen, N, där 1 ≤ N ≤ 2000. Utrymmena är numrerade från 0 till N-1. På den följande raden står två heltal S och Y: numret på utrymmet du befinner dig i från början och numret på utrymmet med nyckeln. Talen uppfyller förstås 0 ≤ S, Y ≤ N-1. Därefter följer N rader med en bokstav på varje rad, antingen i för inomhus eller u för utomhus. Den första raden gäller för utrymme 0, den andra för utrymme 1 o.s.v. Därefter följer ett heltal D, antalet dörrar, där 1 ≤ M ≤ 200000. Slutligen följer M rader med tre heltal P, Q och T och en bokstav (o eller l) på varje rad. Varje rad beskriver en dörr. Talen P och Q är numren på de utrymmen dörren förbinder och T är tiden (i sekunder) det tar att gå igenom dörren. Talen uppfyller 0 ≤ P, Q ≤ N-1 och 1 ≤ T ≤ 1000. Bokstaven betecknar huruvida dören är olåst (o) eller låst (l). Du kan förutsätta att både din startpunkt och nyckeln är inomhus, samt att det alltid finns minst ett sätt att ta sig ut

Utdata

Programmet ska skriva ut det minsta antalet sekunder som du behöver för att ta dig till ett utrymme som är utomhus.

Exempel: Indata

Exempel: Utdata

Lösning[redigera]

Det står nästan i klarspråk att man bör använda kortaste-vägen-algoritmen för denna uppgift. En anmärkningsbar egenskap hos denna uppgift är dess delproblem. Till skillnad från vissa uppgifter som innehåller flera olika deluppgifter så innehåller denna nämligen samma deluppgift flera gånger! Om man tänker efter lite så inser man att svaret kan utformas såhär:

Svar = min( <springa ut direkt>, <springa till nyckeln> + <springa ut från nyckelns position med nyckeln>)

Tre kortaste-vägen alltså. Dijkstra är en lämplig algoritm för att lösa detta problem, som vi redan vet så finns det två versioner av Dijkstra, i detta problem fungerar både varianterna med indatagränserna (kolla detta!). Den pedagogiska poängen med denna uppgift är att lära sig fördelarna med att skriva någorlunda generaliserad kod och undvika att kopiera kod flera gånger. Om du skriver tre olika Dijkstra, så kommer du få stora beskymmer om du ser att du gjort ett misstag någonstans. Givetvis är detta tävlingsprogrammering där din kod ej bedöms efter utseende, dock är det för din egen del mycket viktigt att du har koll på dina kodrader. För att klara denna uppgift krävs det givetvis att du kan skriva en vanlig Dijkstra. Enda modifikationen är att i originalproblemet så finns det bara en slutnod. I detta fall finns det flera möjliga slutnoder, det är alltså en nästan obetydlig modifikation.

Lösningsförslag[redigera]

Koden nedan använder många personliga typedefs och makrofunktioner, vilket kan göra den lite svårläslig för vissa, så försök ej lägga stor möda på att förstå den. Det viktiga är att man själv kan skriva en egen Dijkstra.

#include <iostream>
#include <vector>
#include <sstream>
#include <set>
#include <queue>

using namespace std;

typedef pair < int, int > II;
typedef vector < int > VI;
typedef vector < II > VII;
typedef vector < VII > VVII;
typedef stringstream SS;
typedef set < int > SI;
typedef long long LL;

typedef pair < II, bool > IIB; // dest, cost, keyneeded
typedef vector < IIB > VIIB;
typedef vector < VIIB > VVIIB;

#define sz(c) (int((c).size()))
#define all(c) (c).begin(), (c).end()
#define tr(c, it) for(typeof((c).begin()) it = (c).begin(); it!=(c).end(); it++)
#define sfor(type, e, start, stop) for(type e=start; e<stop; e++)
#define foru(var, stop) sfor(int, var, 0, stop)
#define error(msg) (cout << (msg), throw)
#define ee(a1,a2,a3) IIB(II(a1, a2), a3)

int djikstra(int start, VVII graph, SI slutnoder);
int calc(int start, int key, VVIIB graph, SI slutnoder);

int calc(int start, int key, VVIIB graph, SI slutnoder){
	VVII graph_withkey;
	VVII graph_nokey;
	SI lookforkey; lookforkey.insert(key);
	tr(graph, it){
		VII withkey;
		VII nokey;
		tr(*it, it2){
			II simple_edge = it2 -> first;
			// en simple edge har endast en destination och en kostnad
			if(!it2->second) // behövs nyckel till dörren?
				nokey.push_back(simple_edge);
			withkey.push_back(simple_edge);
		}
		graph_withkey.push_back(withkey);
		graph_nokey.push_back(nokey);
	}
	int gostraight = djikstra(start, graph_nokey, slutnoder);
	int getkey = djikstra(start, graph_nokey, lookforkey);
	int gowithkey = djikstra(key, graph_withkey, slutnoder);
	int getkey_plus_getout = getkey + gowithkey;

	if(gostraight < getkey_plus_getout){
		return gostraight;
	}
	else{
		return getkey_plus_getout;
	}
}

// Här implementeras Dijkstra med prioritetskö
// Notera att ej 3 Dijkstra är implementerade
// (funktionen är felstavad, ja)
int djikstra(int start, VVII graph, SI slutnoder){
	const int alot = 999999999;
	int n = sz(graph);
	VI D(n, alot);
	priority_queue <II, VII, greater< II > > pq;
	// greater< II > gör så att man tar de närmsta bågarna först
	// annars skulle man "sortera baklänges"
	pq.push(II(0, start));
	while(!pq.empty()){
		II elem = pq.top(); pq.pop();
		int ix0 = elem.second; // index
		int cost0 = elem.first;
		if(D[ix0] == alot){
			//first (and only) visit for this node)
			if(slutnoder.count(ix0)) return cost0;
			D[ix0] = cost0;
			tr(graph[ix0], it){
				const II& edge = *it;
				pq.push(II(edge.second + D[ix0], edge.first));
			}
		}
		else if(cost0 < D[ix0]) error("djikstra bug");
	}
	return alot; //if it gets here no exit was found
}


int main(){
	int n;
	cin >> n;
	int start, key;
	cin >> start >> key;
	SI slutnoder;
	foru(i, n) {char temp; cin >> temp; if(temp=='u') slutnoder.insert(i);}
	int T;
	cin >> T;
	VVIIB graph(n);
	foru(i, T){
		int i1,i2,i3;
		char c;
		cin >> i1 >> i2 >> i3 >> c;
		graph[i1].push_back(ee(i2,i3, c =='l'?true:false));
		graph[i2].push_back(ee(i1,i3, c =='l'?true:false));
	}

	cout << calc(start, key, graph, slutnoder) << endl;
}