Matematik för årskurs 7-9/Taluppfattning och räkning/Räkning/Bråktal
| Texten på denna sida saknar en del. Fyll gärna på med mer: Redigera! |
| Det behövs fler uppgifter. Klicka på redigera i någon av de gröna uppgiftsrutorna och lägg till! |
Skriver lite här. I detta kapitlet har jag börjat med övningsuppgifterna och tänkte ta genomgångar och exempel efteråt. Vem som vill får gärna hjälpa till och även lägga in genomgångar och exempel.
Ange tal i bråkform
[redigera]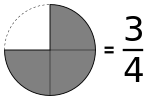
Övningsuppgifter
[redigera]|
Grund-nivå[redigera]1. Ange hur stor del av figurerna som är grå: 2. Skriv som ett bråk talet som har 3 i täljaren och 7 i nämnaren. 3. Vilket bråk är störst:
4. Beräkna:
5. Beräkna:
E-nivå[redigera]5. Ange hur stor del av figurerna som är grå: 6. Ange hur stor del av figurerna som är grå: 7. I en klass gick det 28 elever. I den klassen var det 15 killar. Ange hur stor del av klaasen som var:
8. På en restaurang var en tredjedel av rätterna på menyn kötträtter. Sammanlagt fanns det 15 rätter på menyn.
9. Beräkna:
C-nivå[redigera]A-nivå[redigera]Fördjupning[redigera]Ej nivåsatt[redigera]1. På Donken kom 2 killar och sedan kom 2 tjejer och åt burgare hur många var dom tillslut? 2.
Facit: 2.
|
Förlänga och förkorta bråk
[redigera]
Övningsuppgifter
[redigera]|
Grund-nivå[redigera]1. Förkorta följande bråk med 2:
2. Förkorta följande bråk med 3:
3. Förkorta följande bråk så mycket det går:
4. Förläng följande bråk med 3:
5. Förläng följande bråk så det blir tiondelar:
6. Vilket bråk är störst:
7. Hitta bråken som är lika stora:
E-nivå[redigera]8. Förkorta följande bråk så mycket det går:
9. Ange i enklaste form hur många bollar som är röda: 10. Förläng följande bråk så det blir hundradelar:
11. Förläng följande bråk så det blir samma nämnare:
12. Vilket bråk är störst:
13. Hitta bråken som är lika stora:
C-nivå[redigera]14. Förkorta följande bråk så mycket det går:
15. Förläng följande bråk så det blir hundradelar:
A-nivå[redigera]Fördjupning[redigera]Om man börjar med bråket och sedan tar summan av täljaren och nämnaren (1 + 1) som ett nytt bråks nämnare och sätter den förra nämnaren (1) till täljare så får man . Sedan kan man göra samma sak igen så att man nu får . När man gjort detta många gånger kommer man komma väldigt nära ett tal. Vilket och vad kallas det talet (Googla)? När man håller på med bilder är det ibland intressant att prata om hur höjden och bredden förhåller sig till varandra. Det brukar skrivas som 16:9 eller 4:3. Här är några olika förhållanden som används. Rangordna dem efter hur breda de är i förhållande till sin höjd.
Ej nivåsatt[redigera]
|
Omvandla mellan bråkform och decimalform
[redigera]
För att göra om ett bråktal till decimalform är det bara att räkna som med vanligt division. Man tar då in täljaren delat med nämnaren. Man kan givetvis också räkna ut det med miniräknare. Många bråk går dock inte jämt upp utan kommer ge oändligt många decimalet. En miniräknare avrundar då och om man räknar för hand kan man se när man får samma upprepningar bland decimalerna.
En enkel metod är att kunna några bråktal utantill och sedan använda dem när man ska räkna. Om man exempelvis vet att en fjärdedel är 0,25 måste tre fjärdedelar vara tre gånger så mycket vilket är 0,75. Samma sak i med siffror: → .
De bråken som är lättast att kunna och som används så mycket att de är bra att kunna utantill följer här:
Övningsuppgifter
[redigera]|
Grund-nivå[redigera]E-nivå[redigera]1. Skriv i bråkform och förenkla om det går:
2. Skriv i decimalform:
3. Använd miniräknare (eller om du har gott om tid: beräkna för hand):
4. Det kom en luffare till ett barn och frågade hur många fingrar dom hade tillsammans, vad är svaret? 5. Skriv i decimalform:
C-nivå[redigera]A-nivå[redigera]Fördjupning[redigera]Om man har ett tal där decimalerna upprepar sig (till exempel 0,3333…) så kan de alltid skrivas som ett bråktal.
Antalet siffror som upprepar sig är i detta exemplet bara en (en trea) så vi för länger med 10.
För att bli av med decimalerna kan vi nu ta bort en tiondel av det talet så att vi har nio delar kvar.
0,3333… är alltså samma sak som . Om vi är osäkra kan vi kontrollera med miniräknare och se att ett delat med 3 blir 0,333…. Ibland när man kontrollerar med miniräknare får man dock se upp eftersom sista siffran kan vara avrundad som exempelvis som är 0,666… men som miniräknaren kan visa som 0,6666667. Vi kan prova med ett annat tal: 0,454545… Här förlänger vi med 100 eftersom det är två siffror som upprepar sig.
Sedan tar vi bort en hundradel så vi blir av med decimalerna.
0,454545… är alltså samma sak som . Ibland så tar det ett par decimaler innan talet börjar upprepa sig som till exempel 0,31111…. Då får man ta bort flera delar. Vi visar:
För att bli av med decimalerna måste vi nu ta bort tio hundradelar:
5. Prova själv med exempelvis:
Ej nivåsatt[redigera]
|
Använda blandad form
[redigera]
Ibland när man har bråk som är mer än en hel så delar man upp de talen i två delar. De hela för sig och resten av bråket för sig. Till exempel om man säger en och en halv. Man hade lika gärna kunnat säga tre halvor. När man räknar är det nästan alltid lättast att använda vanlig bråkform men när man pratar i exempelvis recept är det vanligast med blandad form.
Att man använder olika kan förklaras med att man i matematiken skiljer på exakta värden och när det är ungefär medan man i till exempel recept kan köra på känsla och det inte alltid är så noga och inte spelar så stor roll om man tar två och en halv deciliter mjöl i pannkakssmeten eller 2,4 dl mjöl.
För att omvandla från bråkform till blandad form så får man kolla hur många hela bråket räcker till. Om man har bråket så kan man ta 8 av fjärdedelarna och skapa två hela. då har man en fjärdedel över. Hela bråket skrivs då i blandad form som: .
För att göra tvärtom så tar man de hela och omvandlar dem till vad för sorts delar det nu ska vara. Exempelvis i så har vi 3 hela som ska bli femtedelar. En hel blir givetvis fem femtedelar och då blir tre hela alltså 15 femtedelar. Eftersom vi också i själva bråket hade två femtedelar till har vi nu sammanlagt 17 femtedelar. Bråket skrivs alltså i bråkform som .
Övningsuppgifter
[redigera]|
Grund-nivå[redigera]1. Omvandla till bråkform:
E-nivå[redigera]1. Omvandla till bråkform:
2. Omvandla till blandad form:
3. I ett recept till sockerkaka står det att man ska ha två och en halv deciliter socker. Hur många halvdecilitersmått är det? C-nivå[redigera]a) 1 7/6 + 2 4/8 2.
A-nivå[redigera]
Fördjupning[redigera]Ej nivåsatt[redigera]
|
Addera bråk med samma nämnare
[redigera]
Om man har två bråktal och vill addera dem till ett så går det bra om det är samma sorts bråk. Om man till exempel har en tredjedel och adderar med en tredjedel till så kommer man sammanlagt ha två tredjedelar. Om man istället hade en fjärdedel och ska addera en tredjedel så kommer man få två bitar men av olika storlek. Då kan man varken kalla de bitarna för tredjedelar eller fjärdedelar eller något annat.
Så länge det är samma sorts bråk så är det bara att addera täljare med täljare.
När additionen är färdig så kan man behöva förkorta eller skriva om till blandad form om det frågas efter det.
Blandad form
[redigera]Om du skriver ett bråk i blandad form så är det uppdelat i en heltalsdel tillsammans med en kvarlämnad bråkdel. Om man ska addera två bråk där ett eller båda är i blandad form så kan man göra på två sätt. Antingen gör man om de till bråkform och gör additionen som vanligt, eller så adderar man de hela för sig och bråkdelen för sig. Oavsett vilket så måste man sedan efter additionen förenkla och göra om bråket till blandad form om det behövs.
Till exempel:
Metod med att göra om till bråkform:
Metod med att addera för sig:
Övningsuppgifter
[redigera]|
Grund-nivå[redigera]E-nivå[redigera]1. Beräkna:
C-nivå[redigera]2. Beräkna:
A-nivå[redigera]Fördjupning[redigera]Ej nivåsatt[redigera]
|
Addera bråk med olika nämnare
[redigera]
När man har bråk med olika nämnare som ska adderas så går inte det om man inte först omvandlar bråken så att de får samma nämnare.
Om vi exempelvis behöver addera en tredjedel med en fjärdedel så kan vi göra om tredjedelen till fyra tolvtedelar och fjärdedelen till tre tolvtedelar. Nu har vi en addition där båda bråken har samma nämnare (tolvtedelar) och kan alltså addera talen. Svaret blir sju tolvtedelar.
En enkel metod för att få samma nämnare som alltid fungerar är att förlänga det första bråket med det andra bråkets nämnare och att förlänga det andra bråket med det första bråkets nämnare. Ibland kan man vara smartare och förlänga med andra tal så man inte behöver förlänga så mycket. Till exempel kan antingen förlängas till eller till . I första fallet blir svaret och i andra . I båda fallen blir svaret samma men om man var smart och kom på nått bra att förlänga med behöver man inte förkorta så mycket efteråt.
Övningsuppgifter
[redigera]|
Grund-nivå[redigera]E-nivå[redigera]1. Beräkna:
2. Du har två recept på äpplepaj men kan inte bestämma dig för vilket du vill göra så du bestämmer dig för att slå ihop båda och göra en enda stor paj. I det ena receptet står det att man ska ha dl socker och i det andra står det att man ska ha dl. Hur mycket socker ska du ta till din paj?
C-nivå[redigera]A-nivå[redigera]Fördjupning[redigera]3. Beräkna: (tips: börja från vänster och addera ett bråk i taget och se om du ser något mönster)
Ej nivåsatt[redigera]
|
Multiplicera bråk med heltal
[redigera]
När man multiplicerar bråk så behöver man komma ihåg att man multiplicerar nämnare och täljare för sig.
Övningsuppgifter
[redigera]|
Grund-nivå[redigera]E-nivå[redigera]1. Beräkna:
2. Om alla personer på ett kalas äter en halv godispåse var och det är 16 personer på kalaset, hur mycket godis går då åt? 3. Hur mycket rymmer 3 flaskor tillsammans om varje flaska rymmer 3/4 liter?
C-nivå[redigera]A-nivå[redigera]Fördjupning[redigera]Ej nivåsatt[redigera]
|
Multiplicera bråk
[redigera]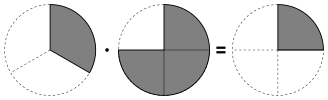
Exempel
[redigera]Räkna ut
Lösning
Nämnarna är 7 och 4, så om man multiplicerar ihop dem så får man 28, täljarna är 3 och 4, om man multiplicerar ihop dem får man 12. Resultatet blir och efter förenkling
Övningsuppgifter
[redigera]|
Grund-nivå[redigera]E-nivå[redigera]C-nivå[redigera]Räkna ut följande tal. 1
2
Facit 1
2
A-nivå[redigera]Fördjupning[redigera]Ej nivåsatt[redigera]
|
Dividera bråk med heltal
[redigera]
Övningsuppgifter
[redigera]|
Grund-nivå[redigera]E-nivå[redigera]C-nivå[redigera]A-nivå[redigera]Fördjupning[redigera]Ej nivåsatt[redigera]
|
Dividera bråk
[redigera]
Övningsuppgifter
[redigera]|
Grund-nivå[redigera]E-nivå[redigera]C-nivå[redigera]A-nivå[redigera]Fördjupning[redigera]Ej nivåsatt[redigera]
|
Länkar
[redigera]Fler digitala matteböcker med genomgångar om negativa tal:
- Matteboken.se - Rationella tal
- Matteboken.se - Förlängning och förkortning av bråk
- Matteboken.se - Addition och subtraktion av bråk
- Matteboken.se - Multiplikation och division av bråk
- Webbmatte.se - Bråk
Wikibooks på engelska:
Mer (avancerad) information om räkesätten finns också på wikipedia:
- Bråk Bra ganska enkel sida.
- Rationella tal Avancerad information
Khan academy (på engelska):
Arcademic skill builders:
Om bildformat:








































































































































