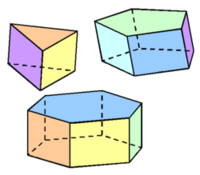
Matematik för årskurs 7-9/Geometri/3D-Geometri/Uppgifter/Prismor

Grund-nivå

<inc>Prismat på bilden har en bottenarea på 10,4 cm² och är 2 cm hög.

Beräkna dess volym.

E-nivå

<inc>Prismat på bilden har en bottenarea på 2.7 cm², sidlägnden 2,5 cm och är 3 cm hög.

a) Beräkna dess volym.

b) Beräkna dess area

<inc>Pentagonen på bilden har en bottenarea på 15,5 cm². Den är 2 cm hög. Beräkna dess volym.

<inc>Ett tält är triangelformat och är 2,20 m långt, 1,60 m brett och 1,20 m högt.

a) Hur många m² tältduk består tältet av?

b) Hur många m³ luft innehåller tältet?

<inc>På bilden är ett prisma. Den skuggade arean är 2 cm2 och den är 2 cm hög. Beräkna volymen.

<inc>En hexagons area är ungefär dess sidlägnd i kvadrat multiplicerat med 2,6. Hexagonen på bilden har en sidlägnd och höjd på 3 cm.

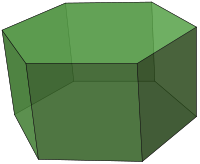
a) Beräkna volymen.

b) Beräkna arean.

C-nivå

<inc>Längs en väg ska ett dike grävas som är V-format. Diket ska vara 1,2 m brett och 80 cm djupt. Vägen är 400 meter lång. Hur mycket jord måste grävas bort?

<inc>En järnvägsräls ser ut som nedan:

a) Beräkna dess genomskärningsarea

b) Beräkna dess volym

<inc>En verklig räl visas nedan

a) Skissa upp dess genomskärningsarea med "verkliga" mått

b) beräkna dess volym

<inc>Göta älv är Sveriges största flod med ett medelflöde på 570 m³/s. Om Göta älv på ett ställe är 100 m bred på 60 m av de 100 är den 8 m djup. En ungefärlig skiss av dess genomskärning visas. Hur fort rinner vattnet där? (Antag att vattnet rinner lika fort vid bottnen som vid ytan)

<inc>Prismat på bilden är 5 cm lång, 4 cm bred och 3 cm hög. I toppen är den hälften så bred som i botten. Beräkna volymen.

A-nivå

Fördjupning

Samma formel för att räkna på prismor som gäller oavsett hur basytan är formad gäller faktiskt också även om höjden inte går rakt upp så länge som genomskärningsytan är likadan hela vägen. Jämför med ett paralellogram där man kan räkna med basen gånger höjden trots att parallellogramet inte går rakt upp. Samma sak gäller här.

Man kan också tänka att man skivar prismat i väldigt tunna skivor som man sedan lägger i en rak hög så att man får ett vanligt prisma. Den metoden kallas integration och kommer användas mycket mer i gymnasiets matematik.

<inc>Beräkna volymen på följande figurer:

a) TODO

Ej nivåsatt

Bilder till uppgifter: