Matematik för årskurs 7-9/Geometri/2D-geometri
| Det behövs fler uppgifter. Klicka på redigera i någon av de gröna uppgiftsrutorna och lägg till! |

Text...
Rektanglar och kvadrater
[redigera]En rektangel består av fyra sidor där de sidorna mittemot varandra alltid är lika långa och parallella (aldrig kommer korsas även om man gör dem jättelånga). Man brukar kalla den långa sidan för längd och den korta för bredd. I bilden ovan så är sidan nedåt bas (förkortas b) och sidan som går uppåt höjd (förkortas h).
En kvadrat är precis som en rektangel fast alla fyra sidorna måste vara lika långa. Eftersom alla sidor är lika långa brukar man inte kalla sidorna för olika saker utan alla heter sida (förkortas s).
Omkrets
[redigera]Omkretsen på en rektangel eller kvadrat är summan av alla sidor.
För rektanglar:
För kvadrater där b=h:
Area
[redigera]Arean på en rektangel och kvadrat är basen gånger höjden. På en kvadrat är de lika långa så där tar man sidan gånger sidan eller sidan upphöjt till 2.
För rektanglar:
För kvadrater där b=h:
Övningsuppgifter
[redigera]| Uppgifter |
|---|
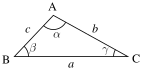
Trianglar
[redigera]Omkrets
[redigera]Area
[redigera]Övningsuppgifter
[redigera]| Uppgifter |
|---|
Parallellogram
[redigera]Omkrets
[redigera]Area
[redigera]Övningsuppgifter
[redigera]| Uppgifter |
|---|
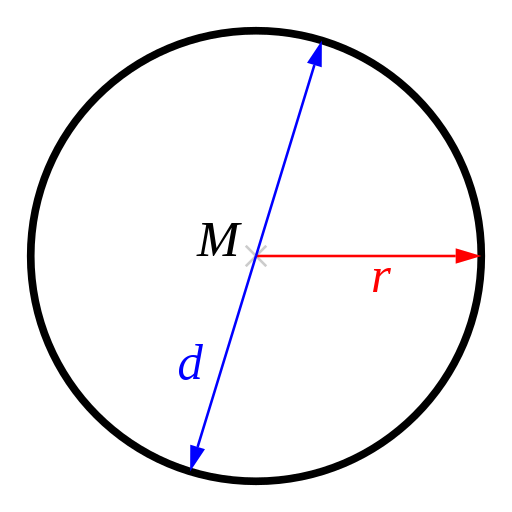
Cirklar
[redigera]Omkrets
[redigera]Omkretsen av en cirkel är diametern (d) multiplicerat med pi (π), d v s Omkrets = d · π eller uttryck med radie som Omkrets = 2 · r · π.
Area
[redigera]
- [1] Geogebra-övning där man bevisar formeln för cirkelns area.
Övningsuppgifter
[redigera]| Uppgifter |
|---|
Blandade figurer
[redigera]Övningsuppgifter
[redigera]| Uppgifter |
|---|
|
Räkna ut omkretsen på en figur som innehåller en triangel och en kvadrat. Kvadratens mått är 4cm och triangelns är 4cm i basen,3cm och 5cm. |