Ellära A
Ellära A[redigera]
Introduktion till kursen[redigera]
Ellära A handlar framförallt om grundläggande samband och storheter inom ellära. Viktiga storheter är spänning, ström, resistans, effekt och energi, viktiga samband är Ohms lag och effektlagen. Kursen tar även upp växelström, elektromagnetiska tillämpningar som elmotorn och transformatorn samt mätteknik.
Skolverkets kursplan säger så här om kursen: "Kursen skall ge grundläggande kunskaper om likström och enfas växelström. Kursen skall också ge kunskaper i mätning, mätvärdesbearbetning och beräkning av elektriska storheter samt utveckla förmågan att välja rätt instrument i olika situationer. Kursen skall dessutom utveckla förmågan att analysera mätvärden och därigenom lägga grunden till felsökning inom el- och elektronikområdet."
Storheter och enheter[redigera]
Spänning[redigera]

Ett enkelt sätt att se på spänning, eller potentialskillnad som det egentligen heter, är att tänka sig två vattenbehållare med en slang mellan sig från botten till botten. Om vattennivån är olika i behållarna (=potentialskillnad) så kommer vatten att flöda i slangen tills nivåerna är lika. När det handlar om elektricitet är slangen den elektriska ledaren (ofta koppar), vattnet är elektroner och de två vattendunkarna kan vara till exempel två poler på ett batteri.
Spänning mäts i enheten volt, som förkortas V.
Ström[redigera]

Elektrisk ström i en ledare är elektroner i rörelse. Om ledarens ena ände är mer negativt laddad, exempelvis om den är kopplad till minuspolen på ett batteri, kommer elektroner att förflytta sig ut i ledningen om ledningen är kopplad till den andra polen. En metalltråd har, som alla andra ämnen en stor mängd elektroner, vilket gör att det är inte de elektroner som kommer från minuspolen som ensamma förflyttar sig genom ledningen, utan de krockar med en elektron i ledaren, som i sin tur krockar med en annan elektron och så vidare, ända tills elektronerna kommer fram till den andra polen.
Ström mäts i enheten ampere, som förkortas A.
Resistans[redigera]
Resistans är ett mått på hur mycket motstånd strömmen har när den ska passera genom en ledare. Ofta beror resistansen på vilket material ledaren består av (egenskapen heter resistivitet), men det kan också vara dåliga anslutningar som gör att resistansen i en krets ökar.
Resistans mäts i ohm, som förkortas Ω.
Energi[redigera]
Energi beskrivs ofta som förmågan att utföra arbete, och elektrisk energi kan vara förmågan att få en lampa att lysa eller en fläkt att snurra.
Energi mäts i joule, som förkortas J. Inom elektrotekniken används oftast i stället för J enheten wattsekund (Ws) och räknar man i tusen Watt som är en kW och tiden i timmar som är 3600 sekunder fås enheten kWh som är faktureringsgrund för vanliga elkonsumenter.
Effekt[redigera]
Effekt är ett mått på hur snabbt energi omvandlas, i en lampa som avger en hög effekt omvandlas elektrisk energi till ljus och värme snabbare än i en lampa som avger låg effekt.
Effekt mäts i watt, förkortat W, som kan definieras som 1 joule per sekund.
Samband och formler[redigera]
Ohms lag[redigera]
där är spänningen i volt, är resistansen i ohm och är strömmen i ampere.
Resistivitet[redigera]
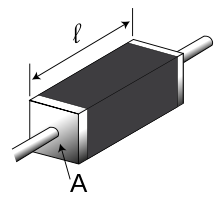
För att räkna ut hur stor resistans något har använder man sig av hur det ser ut och vilket material det är gjort av. För en rak ledare ser uttrycket ut så här:
där är resistansen (Ω) hos ledaren, är materialets resistivitet (Ωm), är ledarens längd (m) och är ledarens tvärsnittsyta (m2).
Följande tabell ger resistiviteten för några utvalda material:
| Material | Resistivitet (Ωm) |
Material | Resistivitet (Ωm) | |
|---|---|---|---|---|
| Silver | 1,59x10-8 | Bly | 2,06x10-7 | |
| Koppar | 1,72x10-8 | Kvicksilver | 9,84x10-7 | |
| Guld | 2,35x10-8 | Kol (grafit) | 1,3x10-5 | |
| Aluminium | 2,65x10-8 | Vatten (destillerat) | 5x108 | |
| Zink | 5,92x10-8 | Glas | 5x1011 | |
| Järn | 9,7x10-8 | Gummi | 5x1013 | |
| Tenn | 1,01x10-7 | Svavel | 2x1015 | |
| Stål | 1,6x10-7 | Plexiglas | 1019 |
Tabellen är sorterad efter ökad resistivitet. Av grundämnena har silver den lägsta resistiviteten och svavel har den högsta. Gäller vid 300 Kelvin vilket är ungefär rumstemperatur.
Ersättningsresistans[redigera]
Ofta behöver man räkna ut hur stor resistansen är för flera sammansatta komponenter. Detta kallas vanligen för ersättningsresistans. För att kunna beräkna en ersättningsresistans måste man oftast dela upp kretsen i flera mindre delar, där delarna är antingen serie- eller parallellkopplade.
Ersättningsresistans vid seriekoppling[redigera]

När man seriekopplar resistorer får strömmen allt svårare att passera ju fler resistorer man ”hakar” på. Följande uttryck kan användas för att beräkna ersättningsresistansen:
Ersättningsresistans vid parallellkoppling[redigera]

När man parallellkopplar resistorer ger vi strömmen fler vägar att komma fram vilket gör att den totala resistansen minskar. Följande uttryck kan båda användas för att beräkna ersättningsresistansen men det andra uttrycket är lite enklare (det första uttrycket kommer från härledningen av uttrycket utifrån Kirchhoffs strömlag, se nedan):
eller
Effektlagen[redigera]
där är effekten i watt, är spänningen i volt och är strömmen i ampere.
Effektlagen kan också skrivas om (med hjälp av Ohms lag) som eller , där man även ser att effekten ökar med kvadraten på strömmen och spänningen!
Kirchhoffs spänningslag[redigera]
Summan av spänningarna i en slinga av en krets ska vara noll
Om summan av spänningarna i en slinga ska vara 0 och vi säger att spänningskällor är positiva och spänningsfall över komponenter är negativa får vi uttrycket eller .
Exempel:
Fråga: Två stycken resistorer på 12 Ω respektive 6 Ω är seriekopplade i serie med ett batteri som har spänningen 9 V. Visa att denna krets uppfyller Kirchhoffs spänningslag?
Lösning: För att kunna visa att denna krets uppfyller Kirchhoffs spänningslag måste vi få fram spänningen över respektive resistor. Spänningarna kan vi få fram genom Ohms lag om vi vet hur stor ström som flyter genom kretsen. Genom att först beräkna en ersättningsresistans för de två resistorerna och därefter använda Ohms lag kan vi få räkna ut hur stor strömmen är. Steg två blir sedan att använda Ohms lag för att beräkna spänningen över respektive resistor:

Spänningsdelning[redigera]
Att beräkna delspänningar med hjälp av spänningsdelning är en tillämpning av Kirchhoffs spänningslag. Ofta handlar det om specialfallet att dela upp en spänning i två delspänningar med hjälp av resistorer:
Kirchhoffs strömlag[redigera]
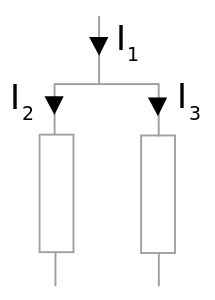
Summan av strömmarna i en nod ska vara noll
Om summan av strömmarna i en nod ska vara 0 får vi uttrycket eller . Detta kan jämföras med en flod som förgrenas - den mängd vatten (el) som strömmar in i en knutpunkt (nod) måste även strömma ut.
Mätteknik[redigera]
Olika mätinstrument[redigera]
Det finns många olika typer av mätinstrument, vilket man använder beror dels på vad man vill mäta, dels på hur noggrant man vill mäta det. Exempel på mätinstrument som ofta används inom elläran:
- multimeter - ett instrument som ofta innehåller alla fyra nedanstående funktioner men ofta med begränsad noggrannhet och snabbhet
- voltmeter - mäter spänning, ofta i området 100 mV - 300 V
- amperemeter - mäter ström, ofta i området 1 mA - 10 A
- ohmmeter - mäter resistans, ofta i området 1 Ω - 200 MΩ. (strömlös krets)
- kontinuitetsmeter - mäter om ledningen är hel, används ofta för att felsöka
- oscilloskop - en avancerad voltmeter som kan mäta med en noggrannhet på någon mV och mäta så ofta som en gång per mikrosekund
- LC-meter - mäter induktans och kapacitans (för spolar och kondensatorer)
Använda mätinstrument[redigera]
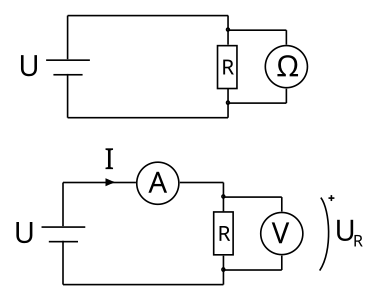
Lik- och växelström[redigera]
Den stora skillnaden mellan lik- och växelström är att i likström rör sig elektronerna åt samma håll hela tiden, medan i växelström byter elektronerna riktning.
Likström[redigera]
Likström, DC (eng. direct current), är elektrisk ström som alltid har samma riktning till skillnad från växelström där strömmen byter riktning. Galvanisk ström är en äldre benämning på likström som i viss mån fortfarande används.
Växelström[redigera]
Om en spänning växlar polaritet, dvs. växlar mellan positiv och negativ spänning, byter strömmen riktning i ledaren. När man beskriver en ström måste man därför tala om vilken riktning som räknas som positiv och vilken räknas som negativ. Diagrammet nedan visar dels hur stor strömmen är vid ett visst tillfälle, men också åt vilket håll den rör sig:
Om strömmen ändrar riktning i ett regelbundet mönster kallas den för periodisk:
För att man på ett enkelt sätt ska kunna tala om hur en periodisk växelström beter sig har man enats om några begrepp:
där
ögonblicksvärdet (momentanvärdet) toppvärdet (maximivärdet, amplituden) vinkelfrekvensen i radianer per sekund tiden fasvinkeln
Sinusformad växelström[redigera]
En mycket vanlig periodisk växelström är den sinusformade växelströmmen. Den hittar vi exempelvis i vårt elnät. En allmän sinusformad växelstorhet kan skrivas
där
ögonblicksvärdet (momentanvärdet) toppvärdet (maximivärdet, amplituden) vinkelfrekvensen i radianer per sekund tiden fasvinkeln effektivvärdet
Tiden för en period, perioden eller periodtiden är
Antalet perioder per sekund, periodtalet eller frekvensen
Enheten för frekvens är hertz (1 Hz).
För en sinusformad växelstorhet är
Elektromagnetism[redigera]
Elektromagnetismen beskriver hur elektricitet och magnetism hänger samman, hur man kan skapa en magnet av ström, men även tvärtom, hur man kan skapa ström från magnetism. Det var flera stora upptäckter i början av 1800-talet, bland annat Ørsteds försök, se nedan, som lade grunden för elektromagnetismen, och än idag är det en stor del av vår teknik som bygger på elektromagnetismen.
Ørsteds försök[redigera]
Vid förberedelsen av ett demonstrationsförsök för en lektion 21 april 1820 lade den danske vetenskapsmannen Hans Christian Ørsted märke till att en kompassnål rörde sig när han slöt en strömkrets i närheten av kompassen. Han började med systematiska experiment och undersökte olika ledare, han såg att kompassnålens vred sig åt andra hållet när han bytte strömriktning, och han visade att effekten inte kunde skärmas av trä eller glas.
Elektromagnetiska tillämpningar[redigera]
För att få en uppfattning av hur man kan använda elektromagnetismen praktiskt använder vi oss av tre olika tillämpningar, elektromagneten, elmotorn/-generatorn och transformatorn.
Elektromagneten[redigera]
Elmotorn/-generatorn[redigera]
Transformatorn[redigera]


































