Matematik/Matematik A/Funktioner
Funktioner
Koordinatsystem[redigera]
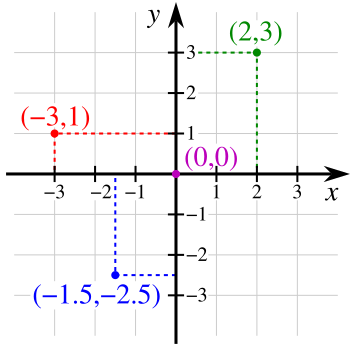
Ett koordinatsystem kan bestå av två linjer som är vinkelräta mot varandra (det kartesiska koordinatsystemet, uppkallat efter den franske filosofen René Descartes). Den horisontella linjen kallas ofta för x-axeln och den vertikala linjen kallas ofta för y-axeln. Oftast har axlarna samma nollpunkt:
En punkt i koordinatssystemet kan beskrivas med två värden, x-koordinaten och y-koordinaten, på formen (x,y). Den gröna punkten i ovanstående koordinatsystem har alltså x-koordinaten 2 och y-koordinaten 3.
Funktionsbegreppet[redigera]
Linjära funktioner[redigera]
Räta linjens ekvation[redigera]
Alla räta linjer i diagram kan beskrivas med en ekvation som har följande utseende:
, där anger hur mycket linjen lutar och anger var linjen skär y-axeln.
I diagrammet nedan finns det tre linjer – den röda och den blå har samma lutning, de är är parallella, och den röda och den gröna skär y-axeln i samma punkt (0,1).
Räkna utan räknare[redigera]
Procent[redigera]
Historia[redigera]
Ordet procent kommer från latin, det språk som talades i romarriket, och står för pro cent vilket ungefär betyder per hundra, eller hundradel. Att använda sig av hundradelar när man ska räkna ut något är en gammal tradition. Redan den romerske kejsaren Augustus använde sig av hundradelar för att räkna ut skatten på sålda varor, (dvs. det som vi idag kallar för moms). Skatten var en hundradel av varans värde .
Eftersom procent är så vanligt har det fått ett eget tecken: % [1]
1 % = 1 procent = 1 hundradel = = 0,01
Som vi ser kan ett och samma tal skrivas på olika sätt. Dessa olika sätt har fått namn:
1 % kallas för procentform, kallas för bråkform och 0,01 kallas för decimalform.
Grundläggande exempel[redigera]
Hur många procent är fyra av hundra? Fyra av hundra är fyra hundradelar, , och det är samma sak som fyra procent, 4 %!
Hur många procent är sju av femtio? Sju av femtio är sju femtiodelar, som kan förlängas med 2 till och det är samma sak som fjorton procent, 14 %.
Procent av något[redigera]
Ofta används procent för att räkna ut saker i vardagen, t.ex. rabatter på kläder, skatt på lönen, ränta på lån osv. Hur ska man då göra?
En vanlig metod är ett göra om talet som man vill veta procent av till hundradelar genom att dividera (dela) det med hundra. Sedan multiplicerar (gångrar) man svaret med så många procent man vill ha.
Praktiska exempel[redigera]
I Linköpings kommun måste alla betala 32 % av sin inkomst i kommunalskatt. Hur stor skatt ska man betala om man har en månadslön på 23000 kr? Enligt metoden ovan tar vi och dividerar lönen med hundra: . Sedan multiplicerar vi med 32 eftersom man ska betala 32 % skatt: . Man ska alltså betala 7360 kr i skatt till kommunen varje månad.
Potenser[redigera]
Exponentialfunktioner[redigera]
| Denna boksida är en s.k. stubb, alltså bara påbörjad. Hjälp Wikibooks genom att skriva mer! |